Crypto Yahtzee

Rolling the dice, peer to peer

19^th Apr. 2020 6 min. read

The first ever recorded match of correspondence chess took place in 1804 in the Netherlands. If you don’t know what “correspondence chess” is, you can imagine it as being some sort of precursor for online gaming – minus the internet of course. Instead, the player’s turns are exchanged via post cards, which means that a match can easily take several months. (A single one, mind you). From a modern software development point of view, one could argue that this is a nightmare both in terms of transaction latency and transport security.

The world of remote gaming has obviously changed, especially in the last two decades. Although peer-to-peer implementations exist (even within the action genre) the majority of today’s multiplayer games are carried out via dedicated, authoritative servers. This approach makes a lot of things simpler, because the game provider has full control over the course of the match: orchestrating the players is less complex and no participant is able to manipulate the game to their own advantage.

However, the idea of playing peer-to-peer like in the old days still lives on and can be applied to modern communication infrastructure. That is especially true for turn-based parlour games like chess or Yahtzee. My most recent toy project was the implementation of a transactionally robust and cryptographically secure mechanism to play the dice game Yahtzee without needing a server that controls everything. I describe the key ideas behind it in the following post and you also find a playable reference implementation on Github. (Be warned about the latter though – it’s a bit geeky and you might find rough edges…)

¹

Game Protocol

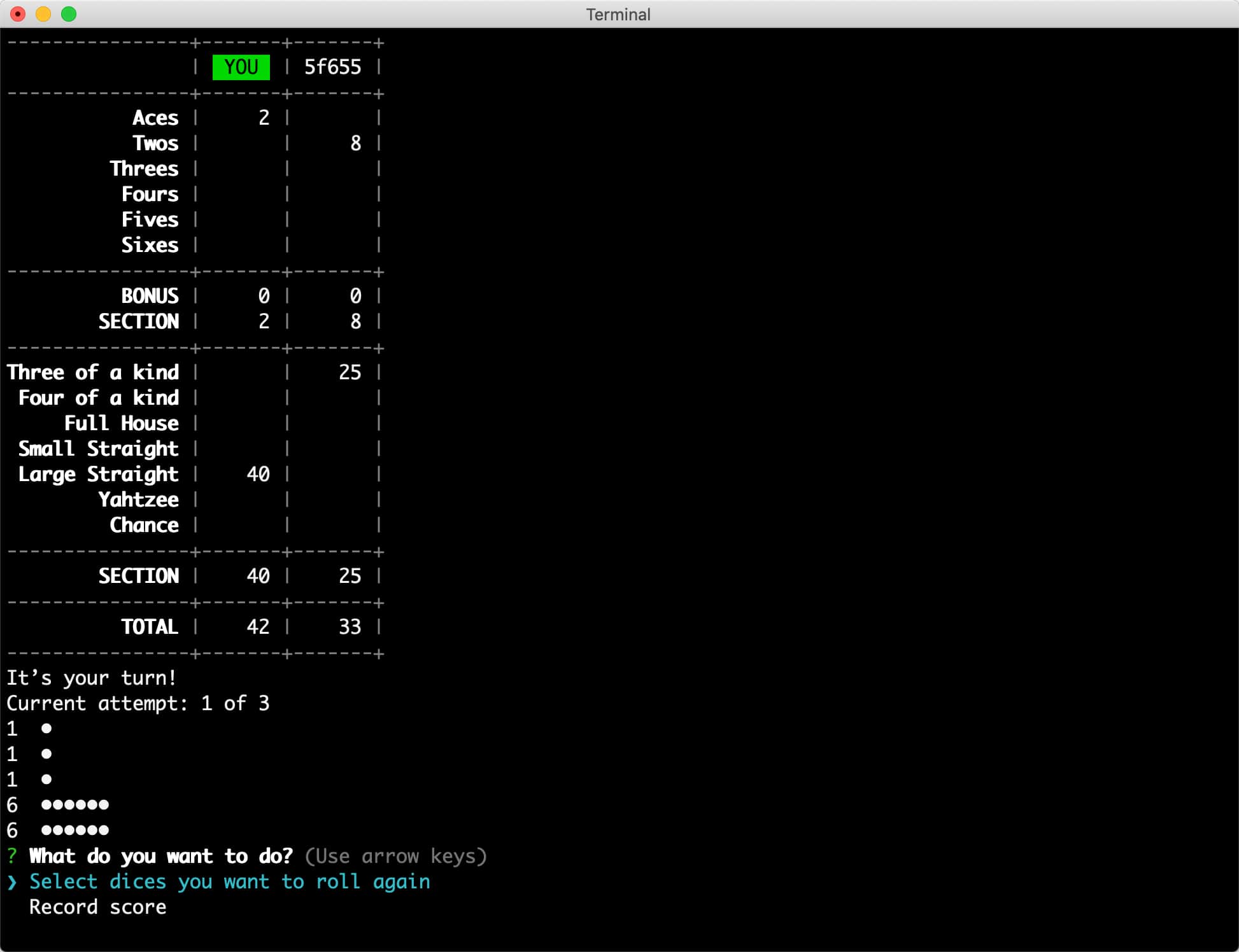
A quick reminder of the rules: Yahtzee² is played with usually a handful of players who take turns one after the other. Every player has three attempts per turn to roll up to five dice, which they need to achieve certain combinations with. (E.g., four in a row, equivalent to a straight in Poker.) The scores are recorded on a scorecard and the game is finished once all 13 categories have been accomplished (or dismissed) by all players.

In a peer-to-peer version there is no game server that could hold and manage the state. Therefore, every player maintains their own copy of the game state and updates it by exchanging transactions with their opponents. In prose, that would read like “I keep the two fours and roll the other dice again” or “I record the current cast with a score of 4 in the ‘aces’ category”. Every player of course has to check for themselves that a received transaction is inline with the game rules and applicable at the respective moment. That should usually be the case, unless there is a malfunctioning client, network problems or an attacker.

Security

Security-wise, there are two problems at hand: how can we be sure that a transaction was issued by a participant of the match and not by some evil “man-in-the-middle”? But even with verified authorship a nasty spoilsport could record transactions of one game and then intersperse them in the next one just to confuse everybody. The answer to these problems are cryptographic signatures and hash chains.

Cryptographic signatures:

Before a match starts, the participants generate asymmetric key pairs and distribute their public key through a trustful source. Transactions get signed by the original author with their (secret) private key. Everyone in posession of the corresponding public key can then verify the authenticity of transmitted data.

Hash chains:

Each player keeps track of all received transactions by appending them to a hash chain. Every transaction contains a checksum (hash) of the preceding transaction, which guarantees definite order. If just a single bit of data within the hash chain got changed, then all subsequent hashes would compute differently. Distinct affiliation to a particular chain can be ensured by including a unique identifier in the root of the chain.

A (simplified) example of a block in such a hash chain could look like this:

// The checksum of the previous block
precedingHash: "70924d6fa4b2d745185fa4660703a5c0"

// Identifier of the issuer (whose public key is known to us)
player: "Joe"

// Joe’s verifiable cryptographic signature of this entire block
signature: "JbY9KlpYmCMAV2I+PRWz9HlKHO3P+QE/WDyTSNXw=="

// Transaction data that will be passed to the game engine
transaction: { action: "record-on-scorecard", category: "threeOfAKind" }

Rolling dice

Checking that someone doesn’t cheat when rolling dice is a no-brainer in real life: you just watch them doing it. That’s obviously not an option in a distributed peer-to-peer setup. Hence, generating a trustably random dice roll that cannot be manipulated requires a multi-step procedure:

1. Every player generates a random bit sequence (called: seed) on their own computer. In the first round, only the hashes of those seeds are shared between all players.
2. Once all players have published their hash, the original seeds are revealed. Everyone can verify that all seeds match up with the previously published hashes and that nothing had been altered after the fact.
3. The seeds (one per player) now get fed into a function that transforms them into a die value (i.e. a number between 1 and 6). The algorithm is a deterministic mapping from list of seeds to die value and always yields the same result for a given set of input seeds.

This procedure must be carried out over and over again for all dice rolls in the match.

One important remark about the hashing: in my implementation the random bit sequences each are 32-bit long. That is problematic, because it makes it easy for players to generate rainbow tables that would allow a reverse lookup. That way a player could quickly tweak their own seed value in order to manipulate the final result as to their desire. There are multiple ways to prevent this – in my case I decided to make use of strong salts, which makes rainbow table generation virtually impossible.

Networking

In a distributed setup there are some pitfalls in regards to networking. This particularly applies to Yahtzee, where the order of turns and actions is more or less predetermined. For instance, if one player is supposed to do something, it’s not allowed for the other players to emit transactions in the meantime until the player on turn has finished.

Imagine the following scenario, however: Alice, Bob and Chris are playing together. Alice is on turn and about to record something on her scorecard. Bob is next up afterwards. Once Alice has made up her mind, she sends her recording transaction to Bob and Chris. However, due to a temporary network glitch, Chris doesn’t receive Alice’s data yet. Bob, on the other hand, gets it and can already proceed starting with his turn. It might occur that Bob’s following action reaches Chris while the previous transaction from Alice is still stuck and hasn’t arrived at Chris yet. To Chris it consequently would appear as if Bob’s action was not valid, because it is based on information that Chris doesn’t know of.

Therefore, it is important that seemingly invalid actions are not outrightly discarded, but rather put on hold somewhere and retried at a later point. Also, when using a push-based transport mechanism (like some messaging system), peers must acknowledge the receipt of transactions among each other, because the recipients have no way to re-obtain data when it has gotten lost along the way.